
Dual basis definition and proof that it's a basis In this video, given a basis beta of a vector space V, I define the dual basis beta* of V*, and show that it's indeed a basis. We'll see many more applications of this concept later on, but this video already shows that it's straightforwar
From playlist Dual Spaces

In this video, I show how to explicitly calculate dual bases. More specifically, I find the dual basis corresponding to the basis (2,1) and (3,1) of R^2. Hopefully this will give you a better idea of how dual bases work. Subscribe to my channel: https://www.youtube.com/c/drpeyam What is
From playlist Dual Spaces

Rings 12 Duality and injective modules
This lecture is part of an online course on rings and modules. We descibe some notions of duality for modules generalizing the dual of a vector space. We first discuss duality for free and projective modules, which is very siilar to the vector space case. Then we discuss duality for finit
From playlist Rings and modules

Definition of V** (double dual) and an amazing miracle Dual Space Definition: https://youtu.be/OGO3HGlOQO4 Dual Spaces Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCs0fJDQnXgeuyFR8iQDwLV Subscribe to my channel: https://www.youtube.com/c/drpeyam
From playlist Dual Spaces

In this video, I show a very neat result about dual spaces: Namely, any basis of V* is automatically a dual basis of some basis of V. Even though this result is very interesting, it's the proof that makes this very exciting, by simply using the fact that V and V** are 'very' isomorphic. En
From playlist Dual Spaces

Dual spaces and linear functionals In this video, I introduce the concept of a dual space, which is the analog of a "shadow world" version, but for vector spaces. I also give some examples of linear and non-linear functionals. This seems like an innocent topic, but it has a huge number of
From playlist Dual Spaces

Understanding the Composition of Two Functions Teacher Explains
Learn how to compose two linear functions. To compose two functions means to express one of the functions as a function of the other function. This is done by replacing the input variable of one of the functions with the value of the second function. We will then simplify the composition a
From playlist How to Compose Two Functions (Linear) #Functions

Learn the Composition of Two Functions
Learn how to compose two functions where one or both of those functions is/are quadratic. To compose two functions means to express one of the functions as a function of the other function. This is done by replacing the input variable of one of the functions with the value of the second fu
From playlist How to Compose Two Functions (Quadratic) #Functions

Introduction to quantized enveloping algebras - Leonardo Maltoni
Quantum Groups Seminar Topic: Introduction to quantized enveloping algebras Speaker: Leonardo Maltoni Affiliation: Sorbonne University Date: January 28, 2021 For more video please visit http://video.ias.edu
From playlist Quantum Groups Seminar

CTNT 2020 - Heuristics for narrow class groups - Benjamin Breen
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Conference Videos
Kazhdan-Lusztig equivalence - Pablo Boixeda Alvarez
Quantum Groups Seminar Topic: Kazhdan-Lusztig equivalence Speaker: Pablo Boixeda Alvarez Affiliation: Member, School of Mathematics Date: May 13, 2021 For more video please visit https://www.ias.edu/video
From playlist Quantum Groups Seminar

Fourier transform for Class D-modules - David Ben Zvi
Locally Symmetric Spaces Seminar Topic: Fourier transform for Class D-modules Speaker: David Ben Zvi Affiliation: University of Texas at Austin; Member, School of Mathematics Date: Febuary 13, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Duality In Higher Categories IV by Pranav Pandit
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Commutative algebra 24 Artinian modules
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We define Artinian rings and modules, and give several examples of them. We then study finite length modules, show that they
From playlist Commutative algebra

Rings 13 Colimits and exactness
This lecture is part of an online course on rings and modules. We discuss the problem of when a colimit of exact sequences is exact. We show that the colimit of exact sequences is at least right exact, but give an example to show that it is not always left exact. We find some conditions u
From playlist Rings and modules

An introduction to modified traces, Jonathan Kujawa, Lecture I
Lecture series on modified traces in algebra and topology The trace of a map and the dimension of a representation are fundamental invariants in representation theory. They are useful both for proving results in representation theory and for applications in other areas (e.g., low-dimensio
From playlist Lecture series on modified traces in algebra and topology

Overview Composition of Functions
Learn how to compose two functions where one or both of those functions is/are quadratic. To compose two functions means to express one of the functions as a function of the other function. This is done by replacing the input variable of one of the functions with the value of the second fu
From playlist How to Compose Two Functions (Quadratic) #Functions

Algebraic geometry 38: The Zariski tangent space (replacement)
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It covers the Zariski tangent space, and describes some other ways of viewing tangent spaces. (This is a replacement for the original video, which had poor audio quality.
From playlist Algebraic geometry I: Varieties
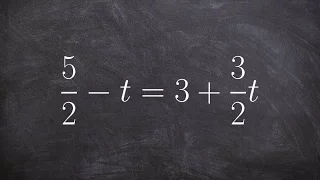
Solving a multi-step equation by multiplying by the denominator
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist How to Solve Multi Step Equations with Variables on Both Sides