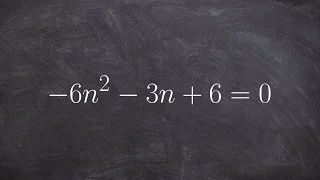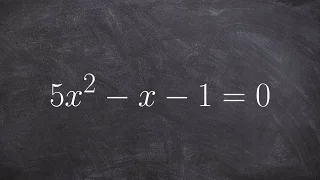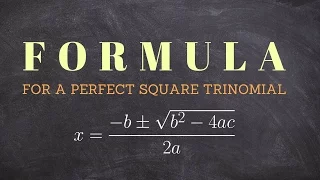Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the (ring of integers of the) algebraic number field. More specifically, it is proportional to the squared volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified. The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic formulas such as the functional equation of the Dedekind zeta function of K, and the analytic class number formula for K. A theorem of Hermite states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem, and the subject of current research. The discriminant of K can be referred to as the absolute discriminant of K to distinguish it from the relative discriminant of an extension K/L of number fields. The latter is an ideal in the ring of integers of L, and like the absolute discriminant it indicates which primes are ramified in K/L. It is a generalization of the absolute discriminant allowing for L to be bigger than Q; in fact, when L = Q, the relative discriminant of K/Q is the principal ideal of Z generated by the absolute discriminant of K. (Wikipedia).