๐ Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
๐ Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
๐ Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
Name the opposite rays in the given figure
๐ Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure
What is a point a line and a plane
๐ Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
Given a line segment name the two planes that intersect
๐ Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure
Naming the rays in a given figure
๐ Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure
What is a point line and plane
๐ Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes
Lecture 11: Discrete Curves (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858
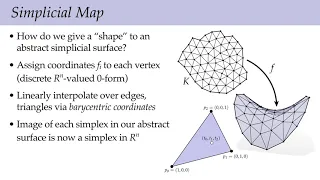
Lecture 14: Discrete Surfaces (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858
Jan Maas : Gradient flows and Ricci cuevature in discrete and quantum probability
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 28, 2017 at the Centre International de Rencontres Mathรฉmatiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry
Oxford Mathematics Roger Penrose Public Lecture: Carlo Rovelli - Spin networks: the quantum structure of spacetime from Penrose's intuition to Loop Quantum Gravity Leading Physicist and best-selling author Carlo Rovelli pays tribute to one of his scientific heroes, Roger Penrose, as he t
From playlist Oxford Mathematics Public Lectures
Konrad Polthier (7/27/22): Boundary-sensitive Hodge decompositions
Abstract: We provide a theoretical framework for discrete Hodge-type decomposition theorems of piecewise constant vector fields on simplicial surfaces with boundary that is structurally consistent with decomposition results for differential forms on smooth manifolds with boundary. In parti
From playlist Applied Geometry for Data Sciences 2022
Neลพa Mramor (2/17/21): An application of discrete Morse theory to robot motion planning
Title: An application of discrete Morse theory to robot motion planning Abstract: We will shortly recollect the basics of discrete Morse theory and two of its variants, parametric and fiberwise discrete Morse theory. We will then describe how it can be used to construct a continuous motio
From playlist AATRN 2021
Sergio Zamora (1/20/23): The lower semi-continuity of \pi_1 and nilpotent structures in persistence
When a sequence of compact geodesic spaces X_i converges to a compact geodesic space X, under minimal assumptions there are surjective morphisms $\pi_1(X_i) \to \pi_1(X)$ for i large enough. In particular, a limit of simply connected spaces is simply connected. This is clearly not true for
From playlist Vietoris-Rips Seminar
Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum), Lecture 1
Quiver moduli spaces are algebraic varieties encoding the continuous parameters of linear algebra type classification problems. In recent years their topological and geometric properties have been explored, and applications to, among others, Donaldson-Thomas and Gromov-Witten theory have
From playlist Felix Klein Lectures 2020: Quiver moduli and applications, Markus Reineke (Bochum)
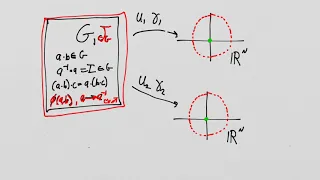
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the concept of a Universal Covering Group
Lie Groups and Lie Algebras: Lesson 38 - Preparation for the Universal Covering Group concept In this lesson we examine another amazing connection between the algebraic properties of the Lie groups with topological properties. We will lay the foundation to understand how discrete invaria
From playlist Lie Groups and Lie Algebras
What does the intersection of lines and planes produce
๐ Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure
Jan Maas: Optimal transport methods for discrete and quantum systems (part 1)
Optimal transport has become a powerful tool to attack non-smooth problems in analysis and geometry. A key role is played by the 2-Wasserstein metric, which induces a rich geometric structure on the space of probability measures. This structure allows to obtain gradient flow structures for
From playlist HIM Lectures 2015