
(ML 7.7.A1) Dirichlet distribution
Definition of the Dirichlet distribution, what it looks like, intuition for what the parameters control, and some statistics: mean, mode, and variance.
From playlist Machine Learning

Math 139 Fourier Analysis Lecture 05: Convolutions and Approximation of the Identity
Convolutions and Good Kernels. Definition of convolution. Convolution with the n-th Dirichlet kernel yields the n-th partial sum of the Fourier series. Basic properties of convolution; continuity of the convolution of integrable functions.
From playlist Course 8: Fourier Analysis
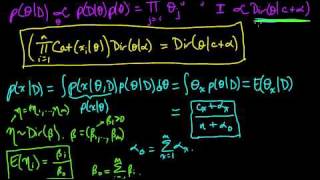
(ML 7.8) Dirichlet-Categorical model (part 2)
The Dirichlet distribution is a conjugate prior for the Categorical distribution (i.e. a PMF a finite set). We derive the posterior distribution and the (posterior) predictive distribution under this model.
From playlist Machine Learning

Properties of Dirichlet Convolution with Prof. Omar!
Part 2 with Prof. Omar: https://youtu.be/8v_sh7JMUS0 Prof. Omar's video covers a very interesting function called the Möbius function, which has special properties related to the Dirichlet convolution. A video on the fall 2014 Caltech-Harvey Mudd Math Competition (CHMMC) power round prob
From playlist Challenge Problems
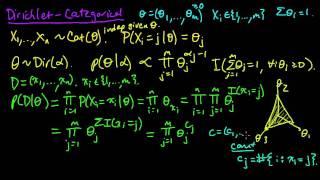
(ML 7.7) Dirichlet-Categorical model (part 1)
The Dirichlet distribution is a conjugate prior for the Categorical distribution (i.e. a PMF a finite set). We derive the posterior distribution and the (posterior) predictive distribution under this model.
From playlist Machine Learning

Dirichlet Eta Function - Integral Representation
Today, we use an integral to derive one of the integral representations for the Dirichlet eta function. This representation is very similar to the Riemann zeta function, which explains why their respective infinite series definition is quite similar (with the eta function being an alte rna
From playlist Integrals

Math 139 Fourier Analysis Lecture 06: Convolutions and Approximations of the Identity, ct'd.
Convolutions and Good Kernels, continued. Interaction of convolution with Fourier transform (for integrable functions). Approximations of the Identity (family of good kernels). Recovery of the value of a function at a point of continuity using approximations of the identity. Uniform co
From playlist Course 8: Fourier Analysis

Differential Equations | Convolution: Definition and Examples
We give a definition as well as a few examples of the convolution of two functions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Adam Skalski: Translation invariant noncommutative Dirichlet forms
Talk by Adam Skalski in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on April 28, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

Introduction to number theory lecture 46. Products of Dirichlet series
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We discuss products of Dirichlet series and show how to use them to prove identities involv
From playlist Introduction to number theory (Berkeley Math 115)

Theory of numbers: Dirichlet series
This lecture is part of an online undergraduate course on the theory of numbers. We describe the correspondence between Dirichlet series and arithmetic functions, and work out the Dirichlet series of the arithmetic functions in the previous lecture. Correction: Dave Neary pointed out t
From playlist Theory of numbers

Francesca Da Lio: Analysis of nonlocal conformal invariant variational problems, Lecture II
There has been a lot of interest in recent years for the analysis of free-boundary minimal surfaces. In the first part of the course we will recall some facts of conformal invariant problems in 2D and some aspects of the integrability by compensation theory. In the second part we will sho
From playlist Hausdorff School: Trending Tools

Math 131 Spring 2022 050422 Riemann-Lebesgue lemma; Classical Fourier Series.
Recall definition of orthonormal systems. Results about General Fourier Series: Proof of "Best Mean Square Approximation" (that the partial sum of the Fourier series of a (Riemann integrable) function is the best linear combination approximating the function in the L2 sense). Consequence
From playlist Math 131 Spring 2022 Principles of Mathematical Analysis (Rudin)

Rings and modules 2: Group rings
This lecture is part of an online course on rings and modules. We decribe some examples of rings constructed from groups and monoids, such as group rings and rings of Dirichlet polynomials. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52XDLrm
From playlist Rings and modules

AMMI 2022 Course "Geometric Deep Learning" - Seminar 1 (Physics-based GNNs) - Francesco Di Giovanni
Video recording of the course "Geometric Deep Learning" taught in the African Master in Machine Intelligence in July 2022 Seminar 1 - Graph neural networks through the lens of multi-particle dynamics and gradient flows - Francesco Di Giovanni (Twitter) Slides: https://www.dropbox.com/s/
From playlist AMMI Geometric Deep Learning Course - Second Edition (2022)

Lecture 16: Fejer’s Theorem and Convergence of Fourier Series
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=8IxHMVf3jcA&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021
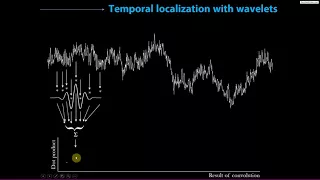
Convolution in the time domain
Now that you understand the Fourier transform, it's time to start learning about time-frequency analyses. Convolution is one of the best ways to extract time-frequency dynamics from a time series. Convolution can be conceptualized and implemented in the time domain or in the frequency doma
From playlist OLD ANTS #3) Time-frequency analysis via Morlet wavelet convolution

Stochastic Homogenization (Lecture 3) by Andrey Piatnitski
DISCUSSION MEETING Multi-Scale Analysis: Thematic Lectures and Meeting (MATHLEC-2021, ONLINE) ORGANIZERS: Patrizia Donato (University of Rouen Normandie, France), Antonio Gaudiello (Università degli Studi di Napoli Federico II, Italy), Editha Jose (University of the Philippines Los Baño
From playlist Multi-scale Analysis: Thematic Lectures And Meeting (MATHLEC-2021) (ONLINE)

Convolution Theorem: Fourier Transforms
Free ebook https://bookboon.com/en/partial-differential-equations-ebook Statement and proof of the convolution theorem for Fourier transforms. Such ideas are very important in the solution of partial differential equations.
From playlist Partial differential equations