Dimensional reduction

Supersymmetry

Dimensional reduction is the limit of a compactified theory where the size of the compact dimension goes to zero. In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions. For example, consider a periodic compact dimension with period L. Let x be the coordinate along this dimension. Any field can be described as a sum of the following terms: with An a constant. According to quantum mechanics, such a term has momentum nh/L along x, where h is Planck's constant. Therefore, as L goes to zero, the momentum goes to infinity, and so does the energy, unless n = 0. However n = 0 gives a field which is constant with respect to x. So at this limit, and at finite energy, will not depend on x. This argument generalizes. The compact dimension imposes specific boundary conditions on all fields, for example periodic boundary conditions in the case of a periodic dimension, and typically Neumann or Dirichlet boundary conditions in other cases. Now suppose the size of the compact dimension is L; then the possible eigenvalues under gradient along this dimension are integer or half-integer multiples of 1/L (depending on the precise boundary conditions). In quantum mechanics this eigenvalue is the momentum of the field, and is therefore related to its energy. As L → 0 all eigenvalues except zero go to infinity, and so does the energy. Therefore, at this limit, with finite energy, zero is the only possible eigenvalue under gradient along the compact dimension, meaning that nothing depends on this dimension. Dimensional reduction also refers to a specific cancellation of divergences in Feynman diagrams. It was put forward by Amnon Aharony, Yoseph Imry, and Shang-keng Ma who proved in 1976 that "to all orders in perturbation expansion, the critical exponents in a d-dimensional (4 < d < 6) system with short-range exchange and a random quenched field are the same as those of a (d–2)-dimensional pure system." Their arguments indicated that the "Feynman diagrams which give the leading singular behavior for the random case are identically equal, apart from combinatorial factors, to the corresponding Feynman diagrams for the pure case in two fewer dimensions." This dimensional reduction was investigated further in the context of supersymmetric theory of Langevin stochastic differential equations by Giorgio Parisi and Nicolas Sourlas who "observed that the most infrared divergent diagrams are those with the maximum number of random source insertions, and, if the other diagrams are neglected, one is left with a diagrammatic expansion for a classical field theory in the presence of random sources... Parisi and Sourlas explained this dimensional reduction by a hidden supersymmetry." (Wikipedia).

Dimensionality Reduction

The code is accesible at https://github.com/sepinouda/Machine-Learning

From playlist Machine Learning Course

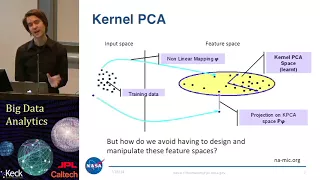
Bala Krishnamoorthy (10/20/20): Dimension reduction: An overview

Bala Krishnamoorthy (10/20/20): Dimension reduction: An overview Title: Dimension reduction: An overview Abstract: We present a broad overview of various dimension reduction techniques. Referred to also as manifold learning, we review linear dimension reduction techniques, e.g., principa

From playlist Tutorials

How can we mitigate the curse of dimensionality?

#machinelearning #shorts #datascience

From playlist Quick Machine Learning Concepts

The concept of “dimension” in measured signals

This is part of an online course on covariance-based dimension-reduction and source-separation methods for multivariate data. The course is appropriate as an intermediate applied linear algebra course, or as a practical tutorial on multivariate neuroscience data analysis. More info here:

From playlist Dimension reduction and source separation

Lecture 14.1 — Dimensionality Reduction Motivation I | Data Compression — [ Andrew Ng ]

From playlist Machine Learning — Andrew Ng, Stanford University [FULL COURSE]

PCA 2: Data manifolds in high-dimensional spaces

From playlist Dimensionality Reduction and PCA

Dimensionality Reduction | Introduction to Data Mining part 14

In this Data Mining Fundamentals tutorial, we discuss the curse of dimensionality and the purpose of dimensionality reduction for data preprocessing. When dimensionality increases, data becomes increasingly sparse in the space that it occupies. Dimensionality reduction will help you avoid

From playlist Introduction to Data Mining

UMAP explained | The best dimensionality reduction?

UMAP explained! The great dimensionality reduction algorithm in one video with a lot of visualizations and a little code. Uniform Manifold Approximation and Projection for all! 📺 PCA video: https://youtu.be/3AUfWllnO7c 📺 Curse of dimensionality video: https://youtu.be/4v7ngaiFdp4 💻 Babyp

From playlist Dimensionality reduction. The basics.

PCA 2: dimensionality reduction

Full lecture: http://bit.ly/PCA-alg We can deal with high dimensionality in three ways: (1) use domain knowledge if available, (2) make an assumption that makes parameter estimation easier, or (3) reduce the dimensionality of the data. Dimensionality reduction can be done via feature sele

From playlist Principal Component Analysis

8.6 David Thompson (Part 6): Nonlinear Dimensionality Reduction: KPCA

From playlist Big Data Analytics - JPL/Caltech

DDPS | Model reduction with adaptive enrichment for large scale PDE constrained optimization

Talk Abstract Projection based model order reduction has become a mature technique for simulation of large classes of parameterized systems. However, several challenges remain for problems where the solution manifold of the parameterized system cannot be well approximated by linear subspa

From playlist Data-driven Physical Simulations (DDPS) Seminar Series

Assaf Naor: Coarse dimension reduction

Recording during the thematic meeting "Non Linear Functional Analysis" the March 7, 2018 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Ma

From playlist Analysis and its Applications

8.4 David Thompson (Part 4): Linear Dimensionality Reduction

From playlist Big Data Analytics - JPL/Caltech

08 Machine Learning: Dimensionality Reduction

A lecture on dimensionality reduction through feature selection and feature projection. Includes curse of dimensionality and feature selection review from lecture 5 and summary of methods for feature projection.

From playlist Machine Learning

DDPS | Neural Galerkin schemes with active learning for high-dimensional evolution equations

Title: Neural Galerkin schemes with active learning for high-dimensional evolution equations Speaker: Benjamin Peherstorfer (New York University) Description: Fitting parameters of machine learning models such as deep networks typically requires accurately estimating the population loss

From playlist Data-driven Physical Simulations (DDPS) Seminar Series

Dimensionality Reduction : Data Science Concepts

Why would we want to reduce the number of features ? And how do we do it ? PCA Video : https://www.youtube.com/watch?v=dhK8nbtii6I LASSO Video : https://www.youtube.com/watch?v=jbwSCwoT51M My Patreon : https://www.patreon.com/user?u=49277905

From playlist Data Science Concepts

The Drinfeld-Sokolov reduction of admissible representations of affine Lie algebras - Gurbir Dhillon

Workshop on Representation Theory and Geometry Topic: The Drinfeld--Sokolov reduction of admissible representations of affine Lie algebras Speaker: Gurbir Dhillon Affiliation: Yale University Date: April 03, 2021 For more video please visit http://video.ias.edu

From playlist Mathematics

Dimensional reduction

Related pages