
The Diagonalization of Matrices
This video explains the process of diagonalization of a matrix.
From playlist The Diagonalization of Matrices

Characterizations of Diagonalizability In this video, I define the notion of diagonalizability and show what it has to do with eigenvectors. Check out my Diagonalization playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCSovHY6cXzPMNSuWOwd9wB Subscribe to my channel: https://
From playlist Diagonalization

Every operator on a finite-dimensional complex vector space has a matrix (with respect to some basis of the vector space) that is a block diagonal matrix, with each block itself an upper-triangular matrix that contains only one eigenvalue on the diagonal.
From playlist Linear Algebra Done Right

This video defines a diagonal matrix and then explains how to determine the inverse of a diagonal matrix (if possible) and how to raise a diagonal matrix to a power. Site: mathispower4u.com Blog: mathispower4u.wordpress.com
From playlist Introduction to Matrices and Matrix Operations

Diagonal Matrices are Freaking Awesome
When you have a diagonal matrix, everything in linear algebra is easy Learning Objectives: 1) Solve systems, compute eigenvalues, etc for Diagonal Matrices This video is part of a Linear Algebra course taught by Dr. Trefor Bazett at the University of Cincinnati
From playlist Linear Algebra (Full Course)

Diagonalizing a symmetric matrix. Orthogonal diagonalization. Finding D and P such that A = PDPT. Finding the spectral decomposition of a matrix. Featuring the Spectral Theorem Check out my Symmetric Matrices playlist: https://www.youtube.com/watch?v=MyziVYheXf8&list=PLJb1qAQIrmmD8boOz9a8
From playlist Symmetric Matrices

Direct Sum definition In this video, I define the notion of direct sum of n subspaces and show what it has to do with eigenvectors. Direct sum of two subspaces: https://youtu.be/GjbMddz0Qxs Check out my Diagonalization playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCSovHY6c
From playlist Diagonalization

Bourbaki - 16/01/2016 - 4/4 - Benoît STROH
Benoît STROH La correspondance de Langlands sur les corps de fonctions, d’après V. Lafforgue La moitié de la correspondance de Langlands sur les corps de fonctions prédit qu’à toute représentation automorphe des points adéliques d’un groupe G on peut associer un système local sur un ouvert
From playlist Bourbaki - 16 janvier 2016

Schemes 21: Separated morphisms
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne.. We define separated and quasi-separated schemes and morphisms, give a few examples, and show that if a scheme has a separated morphism to an affine scheme the
From playlist Algebraic geometry II: Schemes

Bourbaki - 05/11/2016 - 4/4 - Emmanuel PEYRE
Emmanuel PEYRE - Progrès en irrationalité (d’après C. Voisin, J.-L. Colliot-Thélène, B. Hassett, A. Kresch, A. Pirutka, Y. Tschinkel et al.) C. Voisin a inventé une nouvelle méthode pour prouver que des classes de variétés ne sont pas stablement rationnelles, c’est-à-dire que leur produit
From playlist Bourbaki - 05 novembre 2016

Vincent Lafforgue - 2/3 Paramètres de Langlands et cohomologie des champs de G-chtoucas
Pour tout groupe réductif G sur un corps de fonctions, on utilise la cohomologie des champs de G-chtoucas à pattes multiples pour démontrer la correspondance de Langlands pour G dans le sens "automorphe vers Galois''. On obtient en fait une décomposition canonique des formes automorphes cu
From playlist Vincent Lafforgue - Paramètres de Langlands et cohomologie des champs de G-chtoucas

Katharine Turner (12/3/19): Why should q=p in the Wasserstein distance between persistence diagrams?
Title: Why should q=p in the Wasserstein distance between persistence diagrams? Let me count the ways. Abstract: The Wasserstein distance between persistence diagrams is an important generalisation of the bottleneck distance between persistence diagrams. However there is some variation wi
From playlist AATRN 2019

Noncommutative Geometric Invariant Theory (Lecture 2) by Arvid Siqveland
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Julien Grivaux - The Lie algebra attached to a tame closed embedding
Abstract: If X is a smooth closed subscheme of an ambient smooth scheme Y, Calaque, Caldararu and Tu have endowed the shifted normal bundle NX/Y[−1] with a derived Lie algebroid structure. This structure generalizes the Lie algebra structure on the shifted tangent bundle TX[−1] on a smoot
From playlist Algebraic Analysis in honor of Masaki Kashiwara's 70th birthday

Introduction to Homotopy Theory: Part 8- Homotopy in Model Categories
Credits: nLab: https://ncatlab.org/nlab/show/Introduction+to+Homotopy+Theory#homotopy_2 Animation library: https://github.com/3b1b/manim My own code/modified library: https://github.com/treemcgee42/youtube Music: ► Artist Attribution • Music By: "KaizanBlu" • Track Name: "Remembe
From playlist Introduction to Homotopy Theory

Charles Rezk - 4/4 Higher Topos Theory
Course at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/RezkNotesToposesOnlinePart4.pdf In this series of lectures I will give an introduction to the concept of "infinity
From playlist Toposes online

7F Diagonal Triangular Symmetric Matrices
Diagonal, triangular, and symmetric matrices.
From playlist Linear Algebra

Math 060 Linear Algebra 28 111914: Diagonalization of Matrices
Diagonalization of matrices; equivalence of diagonalizability with existence of an eigenvector basis; example of diagonalization; algebraic multiplicity; geometric multiplicity; relation between the two (geometric cannot exceed algebraic).
From playlist Course 4: Linear Algebra

On Voevodsky's univalence principle - André Joyal
Vladimir Voevodsky Memorial Conference Topic: On Voevodsky's univalence principle Speaker: André Joyal Affiliation: Université du Québec á Montréal Date: September 11, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics
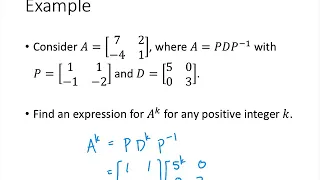
Linear Algebra - Lecture 35 - Diagonalizable Matrices
In this lecture, we discuss what it means for a square matrix to be diagonalizable. We prove the Diagonalization Theorem, which tells us exactly when a matrix is diagonalizable.
From playlist Linear Algebra Lectures