
Statistics: Introduction to the Shape of a Distribution of a Variable
This video introduces some of the more common shapes of distributions http://mathispower4u.com
From playlist Statistics: Describing Data

What is a Sampling Distribution?
Intro to sampling distributions. What is a sampling distribution? What is the mean of the sampling distribution of the mean? Check out my e-book, Sampling in Statistics, which covers everything you need to know to find samples with more than 20 different techniques: https://prof-essa.creat
From playlist Probability Distributions

Uniform Probability Distribution Examples
Overview and definition of a uniform probability distribution. Worked examples of how to find probabilities.
From playlist Probability Distributions

Probability Distribution Functions and Cumulative Distribution Functions
In this video we discuss the concept of probability distributions. These commonly take one of two forms, either the probability distribution function, f(x), or the cumulative distribution function, F(x). We examine both discrete and continuous versions of both functions and illustrate th
From playlist Probability
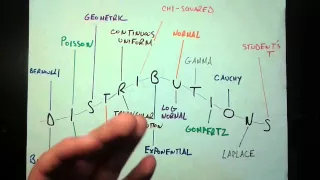
From playlist Probability Distributions

Probability DISTRIBUTIONS for Discrete Random Variables (9-3)
A Probability Distribution: a mathematical description of (a) all possible outcomes for a random variable, and (b) the probabilities of each outcome occurring. Can be tabular (i.e., frequency table) or graphical (i.e., bar chart or histogram). For a discrete random variable, the underlying
From playlist Discrete Probability Distributions in Statistics (WK 9 - QBA 237)

(PP 6.4) Density for a multivariate Gaussian - definition and intuition
The density of a (multivariate) non-degenerate Gaussian. Suggestions for how to remember the formula. Mathematical intuition for how to think about the formula.
From playlist Probability Theory

Binomial and geometric distributions | Probability and Statistics | NJ Wildberger
We review the basic setup so far of a random variable X on a probability space (S,P), taking on values x_1,x_2,...,x_n with probabilities p_1,p_2,...,p_n. The associated probability distribution is just the record of the various values x_i and their probabilities p_i. It is this probabili
From playlist Probability and Statistics: an introduction

Guido Montúfar : Fisher information metric of the conditional probability politopes
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the September 01, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

FRM: Terms about distributions: PDF, PMF and CDF
Distributions characterize random variables. Random variables are either discrete (PMF) or continuous (PDF). About these distributions, we can ask either an "equal to" (PDF/PMF) question or a "less than" question (CDF). But all distributions have the same job: characterize the random varia
From playlist Statistics: Distributions

Random variables describe key things like asset returns. We then use distribution functions to characterize the random variables
From playlist Statistics: Introduction

Learning probability distributions; What can, What can't be done - Shai Ben-David
Seminar on Theoretical Machine Learning Topic: Learning probability distributions; What can, What can't be done Speaker: Shai Ben-David Affiliation: University of Waterloo Date: May 7, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Recursively Applying Constructive Dense Model Theorems and Weak Regularity - Russell Impagliazzo
Russell Impagliazzo University of California, San Diego; Member, School of Mathematics February 7, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

The next building block is mapping transitional probabilities to standard normal variables; then using a bivariate normal to capture joint probabilities of default. For more financial risk videos, visit our website! http://www.bionicturtle.com
From playlist Credit Risk: Portfolio Risk

(PP 6.7) Geometric intuition for the multivariate Gaussian (part 2)
How to visualize the effect of the eigenvalues (scaling), eigenvectors (rotation), and mean vector (shift) on the density of a multivariate Gaussian.
From playlist Probability Theory

Probability functions: pdf, CDF and inverse CDF (FRM T2-1)
[Here is my XLS @ http://trtl.bz/2AgvfRo] A function is a viable probability function if it has a valid CDF (i.e., is bounded by zero and one) which is the integral of the probability density function (pdf). The inverse CDF (aka, quantile function) returns the quantile associated with a pr
From playlist Quantitative Analysis (FRM Topic 2)

FRM: Extreme Value Theory (EVT) - Intro
Extreme value theory (EVT) aims to remedy a deficiency with value at risk (i.e., it gives no information about losses that breach the VaR) and glaring weakness of delta normal value at risk (VaR): the dreaded-fat tails. The key is idea is that the tail has it's own "child" distribution. Fo
From playlist Intro to Quant Finance

Gambling, Computational Information, and Encryption Security - Bruce Kapron
Gambling, Computational Information, and Encryption Security Bruce Kapron University of Victoria; Member, School of Mathematics March 24, 2014 We revisit the question, originally posed by Yao (1982), of whether encryption security may be characterized using computational information. Yao p
From playlist Members Seminar
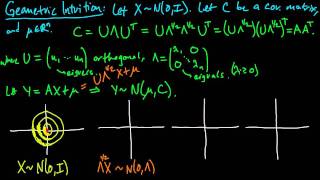
(PP 6.6) Geometric intuition for the multivariate Gaussian (part 1)
How to visualize the effect of the eigenvalues (scaling), eigenvectors (rotation), and mean vector (shift) on the density of a multivariate Gaussian.
From playlist Probability Theory

Computational Entropy - Salil Vadhan
Salil Vadhan Harvard University; Visiting Researcher Microsoft Research SVC; Visiting Scholar Stanford University April 23, 2012 Shannon's notion of entropy measures the amount of "randomness" in a process. However, to an algorithm with bounded resources, the amount of randomness can appea
From playlist Mathematics