Carter subgroup

Finite groups | Subgroup properties | Solvable groups

In mathematics, especially in the field of group theory, a Carter subgroup of a finite group G is a self-normalizing subgroup of G that is nilpotent. These subgroups were introduced by Roger Carter, and marked the beginning of the post 1960 theory of solvable groups. proved that any finite solvable group has a Carter subgroup, and all its Carter subgroups are conjugate subgroups (and therefore isomorphic). If a group is not solvable it need not have any Carter subgroups: for example, the alternating group A5 of order 60 has no Carter subgroups. Vdovin showed that even if a finite group is not solvable then any two Carter subgroups are conjugate. A Carter subgroup is a maximal nilpotent subgroup, because of the normalizer condition for nilpotent groups, but not all maximal nilpotent subgroups are Carter subgroups . For example, any non-identity proper subgroup of the nonabelian group of order six is a maximal nilpotent subgroup, but only those of order two are Carter subgroups. Every subgroup containing a Carter subgroup of a soluble group is also self-normalizing, and a soluble group is generated by any Carter subgroup and its nilpotent residual . viewed the Carter subgroups as analogues of Sylow subgroups and Hall subgroups, and unified their treatment with the theory of formations. In the language of formations, a Sylow p-subgroup is a covering group for the formation of p-groups, a Hall π-subgroup is a covering group for the formation of π-groups, and a Carter subgroup is a covering group for the formation of nilpotent groups . Together with an important generalization, Schunck classes, and an important dualization, Fischer classes, formations formed the major research themes of the late 20th century in the theory of finite soluble groups. A dual notion to Carter subgroups was introduced by Bernd Fischer in. A Fischer subgroup of a group is a nilpotent subgroup containing every other nilpotent subgroup it normalizes. A Fischer subgroup is a maximal nilpotent subgroup, but not every maximal nilpotent subgroup is a Fischer subgroup: again the nonabelian group of order six provides an example as every non-identity proper subgroup is a maximal nilpotent subgroup, but only the subgroup of order three is a Fischer subgroup . (Wikipedia).

Abstract Algebra | Normal Subgroups

We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/

From playlist Abstract Algebra

Subgroups abstract algebra

In this tutorial we define a subgroup and prove two theorem that help us identify a subgroup. These proofs are simple to understand. There are also two examples of subgroups.

From playlist Abstract algebra

GT2. Definition of Subgroup

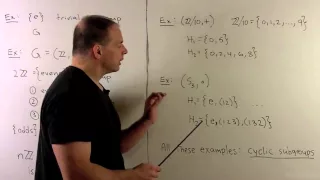
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-

From playlist Abstract Algebra

The BuShou of HanZi :田

A brief description of the BuShou of 田.

From playlist The BuShou of HanZi

The BuShou of HanZi :彳

A brief description of the BuShou of 彳.

From playlist The BuShou of HanZi

Recent developments in non-commutative Iwasawa theory I - David Burns

David Burns March 25, 2011 For more videos, visit http://video.ias.edu

From playlist Mathematics

Abstract Algebra: The definition of a Subgroup

Learn the definition of a subgroup. Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦♦ Ways to support our channel: ► Join our Patreon : https://www.patreon.com/socratica ► Make a one-time PayPal donation: https://www.paypal.me/socr

From playlist Abstract Algebra

Eulerianity of Fourier coefficients of automorphic forms - Henrik Gustafsson

Joint IAS/Princeton University Number Theory Seminar Topic: Eulerianity of Fourier coefficients of automorphic forms Speaker: Henrik Gustafsson Affiliation: Member, School of Mathematics Date: April 30, 2020 For more video please visit http://video.ias.edu

From playlist Mathematics

Multivariate (φ,Γ)-modules by Gergely Zábrádi

PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla

From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Overview of Knots and Motivation of Quandels by Mohamed Elhamdadi

PROGRAM KNOTS THROUGH WEB (ONLINE) ORGANIZERS: Rama Mishra, Madeti Prabhakar, and Mahender Singh DATE & TIME: 24 August 2020 to 28 August 2020 VENUE: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conducted through onl

From playlist Knots Through Web (Online)

Simple Modules for SL2 via BN-Pairs - Lars Thorge Jensen

Seminar on SL2 Topic: Simple Modules for SL2 via BN-Pairs Speaker: Lars Thorge Jensen Affiliation: Member, School of Mathematics Date: October 27, 2020 For more video please visit http://video.ias.edu

From playlist Mathematics

An Euler system for genus 2 Siegel modular forms - David Loeffler

Workshop on Motives, Galois Representations and Cohomology Around the Langlands Program Topic: An Euler system for genus 2 Siegel modular forms Speaker: David Loeffler Affiliation: University of Warwick Date: November 8, 2017 For more videos, please visit http://video.ias.edu

From playlist Mathematics

Normal Subgroups and Quotient Groups (aka Factor Groups) - Abstract Algebra

Normal subgroups are a powerful tool for creating factor groups (also called quotient groups). In this video we introduce the concept of a coset, talk about which subgroups are “normal” subgroups, and show when the collection of cosets can be treated as a group of their own. As a motivat

From playlist Abstract Algebra

Pierre Parent: Stable models for modular curves in prime level

Abstract: We describe stable models for modular curves associated with all maximal subgroups in prime level, including in particular the new case of non-split Cartan curves. Joint work with Bas Edixhoven. Recording during the meeting "Diophantine Geometry" the May 24, 2018 at the Centre

From playlist Algebraic and Complex Geometry

The BuShou of HanZi :宀

A brief description of the BuShou of 宀.

From playlist The BuShou of HanZi

Giles Gardam - Kaplansky's conjectures

Kaplansky made various related conjectures about group rings, especially for torsion-free groups. For example, the zero divisors conjecture predicts that if K is a field and G is a torsion-free group, then the group ring K[G] has no zero divisors. I will survey what is known about the conj

From playlist Talks of Mathematics Münster's reseachers

Groups with bounded generation: properties and examples - Andrei S. Rapinchuk

Arithmetic Groups Topic: Groups with bounded generation: properties and examples Speaker: Andrei S. Rapinchuk Affiliation: University of Virginia Date: October 20, 2021 After surveying some important consequences of the property of bounded generation (BG) dealing with SS-rigidity, the co

From playlist Mathematics

The BuShou of HanZi :目

A brief description of the BuShou of 目.

From playlist The BuShou of HanZi

On exceptional zero conjecture (Mazur-Tate-Teitelbaum) by Srilakshmi Krishnamoorthy

12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.

From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Group Theory: The Center of a Group G is a Subgroup of G Proof

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Group Theory: The Center of a Group G is a Subgroup of G Proof

From playlist Abstract Algebra

Carter subgroup

Related pages