
Polynomials with Trigonometric Solutions (2 of 3: Substitute & solve)
More resources available at www.misterwootube.com
From playlist Using Complex Numbers

In this video, we'll learn how to view a complex number as a 2x2 matrix with a special form. We'll also see that there is a matrix version for the number 1 and a matrix representation for the imaginary unit, i. Furthermore, the matrix representation for i has the defining feature of the im
From playlist Complex Numbers

ComplexMultiplication 1/3 - i/3
From playlist Complex Multiplication

A Swift Introduction to Geometric Algebra
This video is an introduction to geometric algebra, a severely underrated mathematical language that can be used to describe almost all of physics. This video was made as a presentation for my lab that I work in. While I had the people there foremost in my mind when making this, I realiz
From playlist Miscellaneous Math

Injective, Surjective and Bijective Functions (continued)
This video is the second part of an introduction to the basic concepts of functions. It looks at the different ways of representing injective, surjective and bijective functions. Along the way I describe a neat way to arrive at the graphical representation of a function.
From playlist Foundational Math

From playlist Complex Multiplication

GAME2020 3. Professor Anthony Lasenby. A new language for physics. (new audio!)
Cambridge's professor of cosmology and astrophysics Anthony Lasenby takes you through the Geometric Algebra view of all fundamental forces. More information at https://bivector.net This version has updated audio.
From playlist Bivector.net
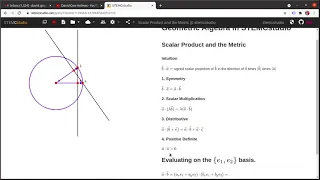
Geometric Algebra, First Course, Episode 06: Scalar Product and the Metric.
The scalar product has many applications in elementary Physics. We extend our Multivector to have the standard scalar product, allowing us to compute magnitudes and angles between vectors. In doing so, we choose our basis vectors to be orthogonal. We recognize that we live in Euclidean Sp
From playlist Geometric Algebra, First Course, in STEMCstudio

Vector form of multivariable quadratic approximation
This is the more general form of a quadratic approximation for a scalar-valued multivariable function. It is analogous to a quadratic Taylor polynomial in the single-variable world.
From playlist Multivariable calculus

QED Prerequisites Geometric Algebra 17 - Bivector products
We examine Bivector-Bivector products using the canonical bivector form. Then we do a bit of bivector-bivector multiplication practice in the second half of the lesson, with a focus on the signature of the resulting product. Please consider supporting this channel on Patreon: https://www
From playlist QED- Prerequisite Topics
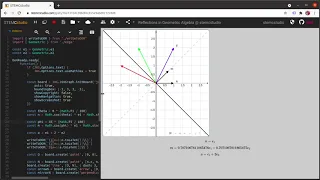
Geometric Algebra, First Course, Episode 12: Rotations
In this video we see how rotations are defined in Geometric Algebra, and meet a new geometric object, the rotor. The rotor will be useful for physics simulations of rigid bodies.
From playlist Geometric Algebra, First Course, in STEMCstudio

Addendum to A Swift Introduction to Geometric Algebra
This video is an addendum to my most popular video, A Swift Introduction to Geometric Algebra. It clears up some misunderstandings that have arisen from the original video, and then describes two useful ways of understanding the geometric product. This also leads to a discussion of the o
From playlist Miscellaneous Math
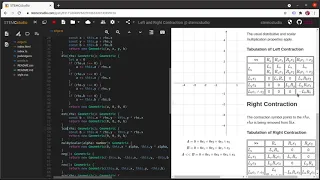
Geometric Algebra, First Course, Episode 07: Left and Right Contraction
We add a new product, the contraction, to our Geometric number that will allow us model the Lorentz Force Law and to factor our a vector from a bivector in a coordinate-free way. The Left Contraction is demonstrated. The Right Contraction is left as an exercise for the viewer.
From playlist Geometric Algebra, First Course, in STEMCstudio

Geometric Algebra, First Course, Episode 08: The Geometric Product.
We finally arrive at the ability to multiply our Geometric numbers together. We see where the geometric product comes from, leading to the definition for vector multiplication, and we add some definitions that allow us to multiply all elements of our algebra. We also use automated testing
From playlist Geometric Algebra, First Course, in STEMCstudio

Pre-Calculus - Multiplying complex numbers (root(14)+root(10) i) (root(14)-root(10) i)
http://www.freemathvideos.com In this math tutorial I will show you how to multiply complex numbers. Complex numbers come in the form of a +bi. Multiplying complex numbers carry some of the same properties as multiplying polynomials. However when simplifying we will notice some differences
From playlist Complex Numbers

QED Prerequisites Geometric Algebra 18: Complex Conjugation (Corrected)
In this lesson we cover the concept of complex conjugation of complex scalars and complex vectors. This version of this lesson has been repaired. The previous version was incorrectly edited. Please consider supporting this channel on Patreon: https://www.patreon.com/XYLYXYLYX The softwar
From playlist QED- Prerequisite Topics

What is the complex conjugate?
What is the complex conjugate of a complex number? Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook
From playlist Intro to Complex Numbers

A Swift Introduction to Spacetime Algebra
This video is a fast-paced introduction to Spacetime Algebra (STA), which is the geometric algebra of Minkowski space. In it, we figure out what the problems are with the way introductory textbooks usually describe special relativity and how we can solve those problems by using spacetime
From playlist Miscellaneous Math

