
Orders on Sets: Part 1 - Partial Orders
This was recorded as supplemental material for Math 115AH at UCLA in the spring quarter of 2020. In this video, I discuss the concept and definition of a partial order.
From playlist Orders on Sets

Set Theory (Part 3): Ordered Pairs and Cartesian Products
Please feel free to leave comments/questions on the video and practice problems below! In this video, I cover the Kuratowski definition of ordered pairs in terms of sets. This will allow us to speak of relations and functions in terms of sets as the basic mathematical objects and will ser
From playlist Set Theory by Mathoma
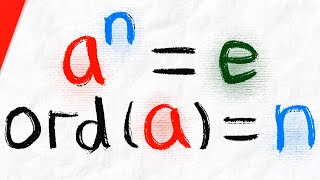
Order of Elements in a Group | Abstract Algebra
We introduce the order of group elements in this Abstract Algebra lessons. We'll see the definition of the order of an element in a group, several examples of finding the order of an element in a group, and we will introduce two basic but important results concerning distinct powers of ele
From playlist Abstract Algebra

Set Theory (Part 2): ZFC Axioms
Please feel free to leave comments/questions on the video and practice problems below! In this video, I introduce some common axioms in set theory using the Zermelo-Fraenkel w/ choice (ZFC) system. Five out of nine ZFC axioms are covered and the remaining four will be introduced in their
From playlist Set Theory by Mathoma

Joseph Bonin: Delta-matroids as subsystems of sequences of Higgs lifts
Abstract: Delta-matroids generalize matroids. In a delta-matroid, the counterparts of bases, which are called feasible sets, can have different sizes, but they satisfy a similar exchange property in which symmetric differences replace set differences. One way to get a delta-matroid is to t
From playlist Combinatorics

Anna De Mier: Approximating clutters with matroids
Abstract: There are several clutters (antichains of sets) that can be associated with a matroid, as the clutter of circuits, the clutter of bases or the clutter of hyperplanes. We study the following question: given an arbitrary clutter Λ, which are the matroidal clutters that are closest
From playlist Combinatorics

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra

Gyula Pap: Linear matroid matching in the oracle model
Gyula Pap: Linear matroid matching in the oracle model Linear matroid matching is understood as a special case of matroid matching when the matroid is given with a matrix representation. However, for certain examples of linear matroids, the matrix representation is not given, and actuall
From playlist HIM Lectures 2015

Field Definition (expanded) - Abstract Algebra
The field is one of the key objects you will learn about in abstract algebra. Fields generalize the real numbers and complex numbers. They are sets with two operations that come with all the features you could wish for: commutativity, inverses, identities, associativity, and more. They
From playlist Abstract Algebra

Nonlinear algebra, Lecture 13: "Polytopes and Matroids ", by Mateusz Michalek
This is the thirteenth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Now that we have defined and understand quotient groups, we need to look at product groups. In this video I define the product of two groups as well as the group operation, proving that it is indeed a group.
From playlist Abstract algebra

The realm of natural numbers | Data structures in Mathematics Math Foundations 155
Here we look at a somewhat unfamiliar aspect of arithmetic with natural numbers, motivated by operations with multisets, and ultimately forming a main ingredient for that theory. We look at natural numbers, together with 0, under three operations: addition, union and intersection. We will
From playlist Math Foundations

Victor Chepoi: Simple connectivity, local to global, and matroids
Victor Chepoi: Simple connectivity, local-to-global, and matroids A basis graph of a matroid M is the graph G(M) having the bases of M as the vertex-set and the pairs of bases differing by an elementary exchange as edges. Basis graphs of matroids have been characterized by S.B. Maurer, J.
From playlist HIM Lectures 2015

Connecting tropical intersection theory with polytope algebra in types A and B by Alex Fink
PROGRAM COMBINATORIAL ALGEBRAIC GEOMETRY: TROPICAL AND REAL (HYBRID) ORGANIZERS Arvind Ayyer (IISc, India), Madhusudan Manjunath (IITB, India) and Pranav Pandit (ICTS-TIFR, India) DATE & TIME: 27 June 2022 to 08 July 2022 VENUE: Madhava Lecture Hall and Online Algebraic geometry is t
From playlist Combinatorial Algebraic Geometry: Tropical and Real (HYBRID)

Yusuke Kobayashi: A weighted linear matroid parity algorithm
The lecture was held within the framework of the follow-up workshop to the Hausdorff Trimester Program: Combinatorial Optimization. Abstract: The matroid parity (or matroid matching) problem, introduced as a common generalization of matching and matroid intersection problems, is so gener
From playlist Follow-Up-Workshop "Combinatorial Optimization"
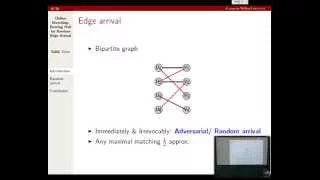
Sahil Singla: Online Matroid Intersection Beating Half for Random Arrival
We study a variant of the online bipartite matching problem that we call the online matroid intersection problem. For two matroids M1 and M2 defined on the same ground set E, the problem is to design an algorithm that constructs the largest common independent set in an online fashion. At e
From playlist HIM Lectures 2015

Centralizer of a set in a group
A centralizer consider a subset of the set that constitutes a group and included all the elements in the group that commute with the elements in the subset. That's a mouthful, but in reality, it is actually an easy concept. In this video I also prove that the centralizer of a set in a gr
From playlist Abstract algebra

Lauren Williams - Combinatorics of the amplituhedron
The amplituhedron is the image of the positive Grassmannian under a map in- duced by a totally positive matrix. It was introduced by Arkani-Hamed and Trnka to compute scattering amplitudes in N=4 super Yang Mills. I’ll give a gentle introduction to the amplituhedron, surveying its connecti
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

[Discrete Mathematics] Indexed Sets and Well Ordering Principle
Today we discuss indexed sets and the well ordering principle. Visit my website: http://bit.ly/1zBPlvm Subscribe on YouTube: http://bit.ly/1vWiRxW *--Playlists--* Discrete Mathematics 1: https://www.youtube.com/playlist?list=PLDDGPdw7e6Ag1EIznZ-m-qXu4XX3A0cIz Discrete Mathematics 2: http
From playlist Discrete Math 1

Galois theory: Transcendental extensions
This lecture is part of an online graduate course on Galois theory. We describe transcendental extension of fields and transcendence bases. As applications we classify algebraically closed fields and show hw to define the dimension of an algebraic variety.
From playlist Galois theory