
Complex analysis: Analytic continuation
This lecture is part of an online undergraduate course on complex analysis. We discuss analytic continuation, which is the extraordinary property that the values of a holomorphic function near one point determine its values at point far away. We give two examples of this: the gamma functi
From playlist Complex analysis

Complex analysis: Holomorphic functions
This lecture is part of an online undergraduate course on complex analysis. We define holomorphic (complex differentiable) functions, and discuss their basic properties, in particular the Cauchy-Riemann equations. For the other lectures in the course see https://www.youtube.com/playlist
From playlist Complex analysis

Positivity and algebraic integrability of holomorphic foliations – Carolina Araujo – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.7 Positivity and algebraic integrability of holomorphic foliations Carolina Araujo Abstract: The theory of holomorphic foliations has its origins in the study of differential equations on the complex plane, and has turned into a powerful t
From playlist Algebraic & Complex Geometry

Math 131 Spring 2022 042722 Properties of Analytic Functions, continued
Recall: analytic functions are infinitely (term-by-term) differentiable. Relation of coefficients and values of derivatives. Remark: analytic functions completely determined by values on an arbitrarily small interval. Analytic functions: convergence at an endpoint implies continuity the
From playlist Math 131 Spring 2022 Principles of Mathematical Analysis (Rudin)

Complex analysis: Singularities
This lecture is part of an online undergraduate course on complex analysis. We discuss the different sorts of singularities of a holomorphic function (removable singularities, poles, essential singularities, branch-points, limits of singularities, natural boundaries) and give examples of
From playlist Complex analysis

Math 135 Complex Analysis Lecture 07 021015: Analytic Functions
Definition of conformal mappings; analytic implies conformal; Cauchy-Riemann equations are satisfied by analytic functions; partial converses (some proven, some only stated); definition of harmonic functions; harmonic conjugates
From playlist Course 8: Complex Analysis

Tangential Lipschitz Gain for Holomorphic Functions - Sivaguru Ravisankar
Sivaguru Ravisankar The Ohio State University; Member, School of Mathematics October 1, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Miroslav Englis: Analytic continuation of Toeplitz operators
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Analysis and its Applications

Analytic continuation in higher dimensions
In this short lecture I will prove the Hartogs theorem stating that holomorphic functions can be continued across compacts subsets if the dimension is at least 2. The proof will use solution of the del bar problem with compact support. For more details see Section 2.3 in Hormander's "Intro
From playlist Several Complex Variables
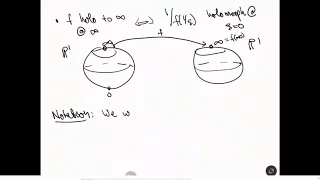
MATH 331: Compactifying CC - part 4 - Endomorphisms of PP^1 are Rational
In this video we finally prove that holomorphic maps from PP^1 to itself are rational.
From playlist The Riemann Sphere

On local interdefinability of analytic functions - T. Servi - Workshop 3 - CEB T1 2018
Tamara Servi (Université Paris-Diderot) / 27.03.2018 On local interdefinability of (real and complex) analytic functions Given two (real or complex) analytic functions f and g, it is not sensible in general to ask whether they are first-order interdefinable as total functions (think of t
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Holomorphic rigid geometric structures on compact manifolds by Sorin Dumitrescu
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

MATH 331: Compactifying CC - part 3 - Functions to PP^1
We describe three compactifications of the complex numbers: The one point compactification, the Riemann Sphere and the complex projective line. In a subsequent video we explain the following facts: *Why all holomorphic functions on the compactification are constant. *Why endomorphism of PP
From playlist The Riemann Sphere

What are domains of holomorphy?
We define domains of holomorphy in C^n. We introduce holomorphically convex domains. We state the Cartan-Thullen theorem, and list consequences. One if them provides the existence of a smallest domain of holomorphy containing a fixed domain. For more details see Hormander's "An introducti
From playlist Several Complex Variables

https://www.math.ias.edu/files/media/agenda.pdf More videos on http://video.ias.edu
From playlist Mathematics

Analytic Continuation and the Zeta Function
Where do complex functions come from? In this video we explore the idea of analytic continuation, a powerful technique which allows us to extend functions such as sin(x) from the real numbers into the complex plane. Using analytic continuation we can finally define the zeta function for co
From playlist Analytic Number Theory

Maxim Konsevitch - 4/4 Exponential Integral
Summary : https://indico.math.cnrs.fr/getFile.py/access?resId=0&materialId=3&confId=694
From playlist Maxim Konsevitch - Exponential Integral
