
Nonparametric additive regression – Byeong Park – ICM2018
Probability and Statistics Invited Lecture 12.4 Nonparametric additive regression Byeong Park Abstract: In this article we discuss statistical methods of estimating structured nonparametric regression models. Our discussion is mainly on the additive models where the regression function (
From playlist Probability and Statistics

Linear regression (5): Bias and variance
Inductive bias; variance; relationship to over- & under-fitting
From playlist cs273a

Determine the Additive Inverses
This video explains how to determine the additive inverse of a given integers. http://mathispower4u.com
From playlist Sets of Numbers/Properties of Real Numbers

Inna Entova-Aizenbud: Jacobson-Morozov Lemma for Lie superalgebras using semisimplification
I will present a generalization of the Jacobson-Morozov Lemma for quasi-reductive algebraic supergroups (respectively, Lie superalgebras), based on the idea of semisimplification of tensor categories, which will be explained during the talk. This is a joint project with V. Serganova.
From playlist Workshop: Monoidal and 2-categories in representation theory and categorification

👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Frobenius exact symmetric tensor categories - Pavel Etingof
Geometric and Modular Representation Theory Seminar Topic: Frobenius exact symmetric tensor categories Speaker: Pavel Etingof Affiliation: Massachusetts Institute of Technology Date: May 12, 2021 For more video please visit https://www.ias.edu/video
From playlist Seminar on Geometric and Modular Representation Theory

Modular Representation Theory: Week Six
30 March 2023 Presented by Chris Hone.
From playlist Modular Representation Theory

Generic bases for cluster algebras (Lecture 3) by Pierre-Guy Plamondon
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Representation theory: Introduction
This lecture is an introduction to representation theory of finite groups. We define linear and permutation representations, and give some examples for the icosahedral group. We then discuss the problem of writing a representation as a sum of smaller ones, which leads to the concept of irr
From playlist Representation theory

How do we multiply polynomials
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Ben Elias: Categorifying Hecke algebras at prime roots of unity
Thirty years ago, Soergel changed the paradigm with his algebraic construction of the Hecke category. This is a categorification of the Hecke algebra at a generic parameter, where the parameter is categorified by a grading shift. One key open problem in categorification is to categorify He
From playlist Workshop: Monoidal and 2-categories in representation theory and categorification

Thorsten Heidersdorf: On fusion rules for supergroups
I will report on some recent progress to understand the indecomposable summands in tensor products of irreducible representations of an algebraic supergroup. I will focus on the $GL(m|n)$ and $OSp(m|2n)$-case.
From playlist Workshop: Monoidal and 2-categories in representation theory and categorification

Why does the distributive property Where does it come from
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

Kevin Coulembier: Frobenius exact tensor categories
Abstract: Partly motivated by Grothendieck’s original vision for motives, the question arises of when a tensor category (k-linear symmetric monoidal rigid abelian category) is tannakian, i.e. is the representation category of an affine group scheme, or more generally of a groupoid in schem
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)
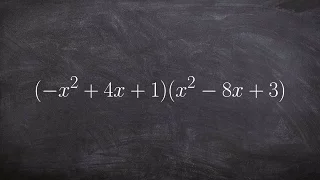
Easiest Way to Multiply Two Trinomials by Each Other - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply a Trinomial by a Trinomial

Identify Addition Properties of Real Numbers
This video explains and provides examples of the properties of real numbers. http://mathispower4u.com
From playlist Number Sense - Properties of Real Numbers

A geometric model for the bounded derived category of a gentle algebra, Sibylle Schroll, Lecture 1
Gentle algebras are quadratic monomial algebras whose representation theory is well understood. In recent years they have played a central role in several different subjects such as in cluster algebras where they occur as Jacobian algebras of quivers with potentials obtained from triangula
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Using the Box Method to Multiply a Trinomial by a Trinomial - Math Tutorial
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply a Trinomial by a Trinomial
Representation Theory & Categorification - Catharina Stroppel
2021 Women and Mathematics - Uhlenbeck Course Lecture Topic: Representation Theory & Categorification Speaker: Catharina Stroppel Affiliation: University of Bonn Date: May 24, 2021 For more video please visit https://www.ias.edu/video
From playlist Mathematics
